(Update 3/8: I originally completely forgot to talk about what happens with different winrates. I added this analysis to the bottom of the post.)
In two of my previous posts (1 2), I crunched some numbers to show that the variance in large-field MTTs is pretty damn crazy. Now I’m going to turn my attention to NLHE 6-max cash games. (Sorry for the delay. I could claim to have been busy, but mostly I’ve just been lazy.)
This is actually pretty easy thanks to the statistician’s best friend, the central limit theorem. For sample sizes of at least a few thousand hands, you can just take your standard deviation and winrate and use the normal approximation. (For sample sizes of less than a few thousand hands…. Who cares?) This makes the math really easy, and in a way, it’s responsible for the relatively cushy lifestyle of cash players–The normal distribution is a lot cleaner than the distribution that I found for MTT players. (Proof that the distribution is normal)
(Another consequence of this mathematical convenience is the fact that some other people have done this analysis already. While my posts on MTTs were, as far as I know, the first honest attempt at tackling that problem correctly, this post will mostly just explain what’s already known to the nerdy contingent of the poker world and anyone else with a basic understanding of statistics. I’m just bothering to share this information with our less nerdy brethren in a way that I feel is reasonably clear. To that end, I’ll mostly just leave out any explanations, but suffice it to say that all of this comes from very basic facts about the normal distribution. However, I think everybody who plays poker should be able to do some basic statistics, so I might make a tutorial explaining where these numbers come from at some point.)
To see how that works out in practice, let’s look at a basic example. Take a solid 6-max NLHE grinder with a 5 bb/100 win rate (I’m going to use bb/100, not PTBB/100 in this post. An unfortunate tradition ported from LHE leads many people–including PTR, PT3, and sometimes me–to call a BB or a PTBB twice a bb.) with a fairly typical standard deviation of 90 bb/100. What happens if 10,000 clones of this guy play 50,000 hands each? Well, this does:
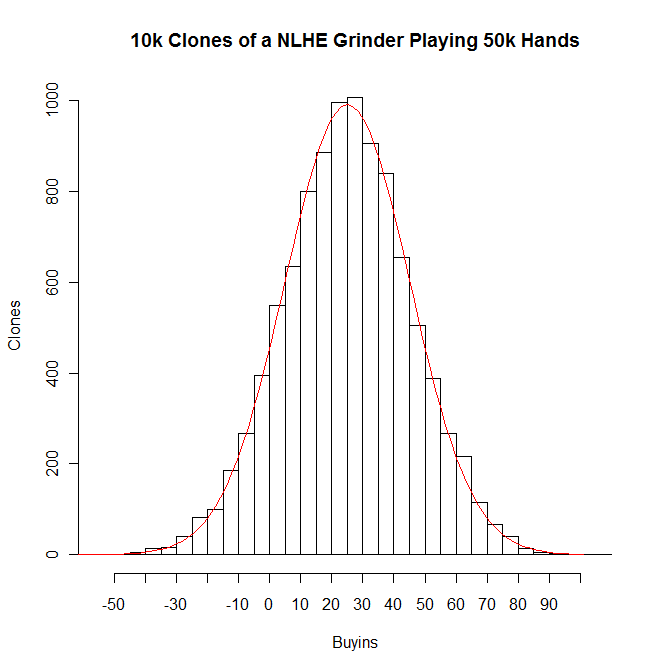
The clones each have an expected value of 25 buyins, and a full 38% of them fall within 10 buyins of their EV. About 47% of them fall between .5x and 1.5x of their equity (i.e. between 12.5 and 37.5 buy-ins). Only 11% of them lose over the sample, and (since this distribution is symmetrical), 11% earn over 50 buy-ins.
Compare this to a roughly similar situation from my MTT data: A 40% ROI player playing 1000 tournaments. The MTT player has a 29% chance of losing and a 23% chance of earning at least twice his equity over that sample. He has only a 34% chance of earning between between .5x and 1.5x his equity, with a significantly higher chance of falling below this range than above it. So, the picture is certainly much better for the cash pro than the MTT pro.
Of course, an 11% chance of loss certainly isn’t negligible. If you play 50k hands/month (which is fairly normal for a decent grinder and takes roughly 25 hours per week if you 6-table) every month for a year, you’ll have one or two losing months in a typical year. (I guess since this post is about stats, I’ll just give the numbers: You’ll have a 25% chance of having no losing months, a 36% chance of having one losing month, a 25% chance of having two losing months, and a 14% chance of having three or more.) That obviously isn’t ideal, and many people would probably accept a much lower salary to get a steady biweekly paycheck instead. But, I imagine that this would be tolerable for most people in the poker world.
While a 50k hand sample ain’t too bad for making money, it’s absolutely terrible for estimating your winrate. A break-even player will find that he has at least a 2 bb/100 winrate over a 50k 31% of the time, and similarly, a 4 bb/100 player will find that he has less than a 2 bb/100 winrate over 50k hands 31% of the time. In other words, if you run at 2 bb/100 over 50k hands, it’s quite plausible that you’re a really solid player, and it’s also quite plausible that you suck. A 95% confidence interval for your winrate over 50k hands is going to span about 16 bb/100 (e.g. -8 bb/100 to 8 bb/100). So obviously your winrate over 50k hands doesn’t really say much.
What if our clones play 200k hands instead?
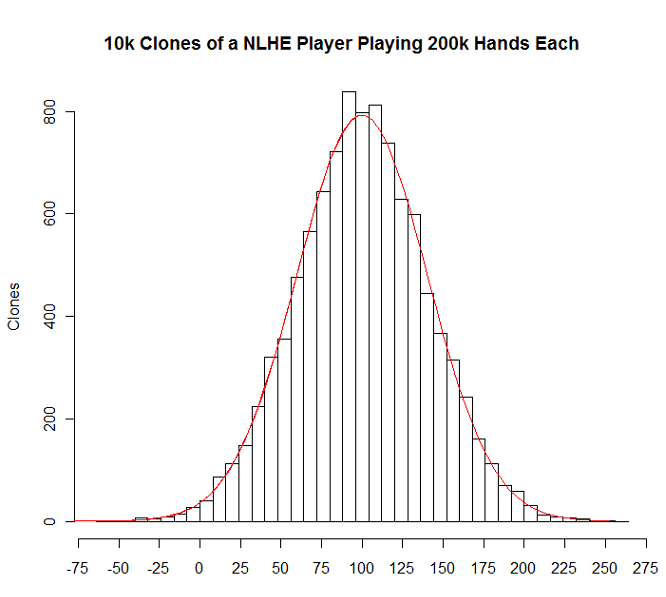
Less than 1% of them lose (0.65%), and almost 90% of them (89.2%) make at least 50 buy-ins. So, a 200k hand sample for a solid NLHE 6-max reg is going to turn out pretty well almost always. That’s awesome. It isn’t the end of the world to play 200k hands–Just 6-table for 400 hours.
Unfortunately, 200k hands still ain’t too great for estimating your winrate; a 95% confidence interval on your winrate over 200k hands still spans about 8 bb/100 (e.g. 0 bb/100 to 8 bb/100), and the 67% confidence interval spans about 4 bb/100 (e.g. 0 bb/100 to 4 bb/100). That’s obviously pretty useless; an 8 bb/100 range is the difference between a slight fish and the best players at mid stakes, and a 4 bb/100 range is the difference betweeen a decent grinder and the best player. So, while a 200k sample might tell you with pretty high confidence that you’re a winner (if you run fairly well or are really good), it won’t tell you much beyond that.
In fact, estimating your winrate accurately is basically impossible. In order to know your winrate at NLHE 6-max within 2 bb/100 (e.g.4 bb/100 +/- 2 bb/100 a.k.a. 2 bb/100 to 6 bb/100) with 95% confidence, you need to play about 800k hands! That’s more hands than I’ve played lifetime (and +/- 2 bb/100 isn’t so great, anyway). So, unless you’re one of the few sickos in the world who plays that amount of hands in a couple months, there’s basically no point in trying to statistically estimate your 6-max NLHE winrate to any reasonable degree of accuracy; the games that you’re playing will likely have changed dramatically before your sample size is significant.
(You can improve the statistics a little bit by using your AIEV bb/100 instead of your real bb/100. When I do that with my own data, it shrinks confidence intervals by about 25%. That’s wonderful, but it’s just not enough. You still need something like 700k hands or so to get a 95% confidence interval of +/- 2 bb/100. Over 200k hands, the 95% confidence interval spans 6 bb/100.)
I suppose you could try estimating your winrate in some other way. You could, for example, take a group of players that you think all are of a similar skill level to you and all play in the same games as you and take their combined winrate over the past couple months. If you play micro, low, or mid stakes on Stars or FTP, you could probably get a 1M+ hands together that way. Similarly, you could take the winrate of the average professional in the games that you play and assume that your winrate is the same (or maybe a bit lower or higher if you think you’re worse or better than average). But, both of these require you to estimate your own skill level and the skill level of others. That’s sort of circular, and it’s also just really hard–One of the main reasons that poker is so profitable is that people are terrible at estimating their own poker skill.
So, estimating your own winrate accurately is pretty much impossible. What this means is that you should be very cautious when you predict your future earnings. Always make sure that you’ll be ok financially if your winrate turns out to be much lower than it has been AND you run really bad over the next 100k hands. If you don’t have that type of financial cushion, you might consider getting staking, playing lower, or doing something else for a living.
Update 3/8:
Oops. I forgot to look at what happens as I vary winrate. So, here’s what happens:
| Winrate (bb/100) | Hands | Equity (Buyins) | Chance of Loss | Chance of < Half Equity |
| 1 | 10000 | 1 | 45.6% | 47.8% |
| 1 | 50000 | 5 | 40.2% | 45.1% |
| 1 | 250000 | 25 | 28.9% | 39.1% |
| 2 | 10000 | 2 | 41.2% | 45.6% |
| 2 | 50000 | 10 | 31.0% | 40.2% |
| 2 | 250000 | 50 | 13.3% | 28.9% |
| 4 | 10000 | 4 | 32.8% | 41.2% |
| 4 | 50000 | 20 | 16.0% | 31.0% |
| 4 | 250000 | 100 | 1.3% | 13.3% |
| 6 | 10000 | 6 | 25.2% | 36.9% |
| 6 | 50000 | 30 | 6.8% | 22.8% |
| 6 | 250000 | 150 | 0.04% | 4.8% |
| 10 | 10000 | 10 | 13.3% | 28.9% |
| 10 | 50000 | 50 | 0.6% | 10.7% |
| 10 | 250000 | 250 | 0.000001% | 0.3% |
So, if you’re a 2 bb/100 winner you lose 31% of the time over 50k hands and 13.3% of the time over 250k hands. That’s already pretty gross, but a 1 bb/100 winner loses 28.9% of the time over 250k hands. That’s just brutal. So, if you’re a very marginal winner in these games, you should probably move down or do something else if you like your sanity. In contrast, if you’re crushing small stakes at 10 bb/100 (a.k.a. 5 PTBB/100, which a few people still manage), life’s pretty sweet. Even over 10k hands, you only lose 13.3% of the time, and a 50k+ hand sample for a 10 bb/100 winner has near-guaranteed profit–and even a nearly 90% chance of making at least 25 buyins. So, a 2 bb/100 winner loses over 250k hands as often as a 10 bb/100 winner loses over 10k hands. How nuts is that? (There’s actually a very simple mathematical explanation.) Even if your winrate is just 6 bb/100 (which some players still pull off at high stakes), things are pretty cushy–You’ll lose about a quarter of the time over 10k hands and only 7% of the time over 50k hands.
So, I suppose there are two major lessons to take away from this article:
- NLHE 6-max variance is a much much smaller deal than large-field MTT variance. The two aren’t even really comparable.
- Estimating your winrate at NLHE 6-max accurately is essentially impossible.
- Having a high winrate at NLHE 6-max is pretty fun.
- Having a low winrate at NLHE 6-max sucks.
Anyway, that’s my rant; hope you liked it. You can bug me on twitter or in the comments if you’d like to know something that I didn’t include (and you can follow me on twitter if you’d like to know when I post next).
I’ll talk about variance in other types of games in future posts, including but maybe not limited to PLO, HU, FR, LHE, and STTs. I also plan to talk about bankroll requirements at some point. Maybe I’ll do BR stuff for MTTs and 6-max cash next and then worry about the other games. Let me know what you’d like to see.
Hey Noah,
great work, with your post about MTT variance and my current downswing i am thinking about switching to cashgames. I am looking forward to posts about PLO SH and BR requirements for the different games.
Thanks.
Hi Noah,
really enjoy reading your blog, really outstandingly interesting.
One question regarding your 6max calculations: Did you factor in rake? If you didn’t, these numbers look a lot worse…
Regards,
Djerzinski
Djerzinski,
Yep. Rake’s included.
Hey Noah, great post- Thank you.
What about including a standard 27% rakeback in your calculations? This would make these numbers a lot nicer and would help the accuracy of them as any full time cash game player has some form of rakeback.
Bryce
Hi Blaaa,
Rakeback will lower your standard deviation a little bit, but the effect won’t be very large at all. Obviously it can help your winrate a lot, though, especially at lower stakes.
So, you can just consider your winrate including rakeback, and the math should work out almost exactly the same. (Now that I actually remembered to include the winrate table, you can just look up your winrate including rakeback in the table and see.)
Any chance at looking at triple draw? Everyone says the variance is crazy and I can attest to that. Don’t know if u have the resources to get hands and a program to analyze though
Noah,
Good post, one thing that doesn’t seem to get mentioned when people do this type of analysis is the non-normal nature of NLHE winrate distribution. Over small sample sizes the distribution is going to have a positive kurtosis (a lot of small pots and a disproportionate number of fat tails). For extremely large sample sizes the central limit theorem is still going to hold but for smaller sample sizes, like the 10k sample and probably the 50k sample as well, you’ll see more extreme events than would be predicted when modeling using the assumption of a normal distribution.
Alex,
I’ll look at triple draw if you get me some triple draw hands and a program that will convert them into data for me. I don’t think there’s anything that does that, is there?
Kerpowski,
Good question. I thought that this deserved a longer answers, so I wrote one up. Let me know what you think.
The cliffs is that a 5k+ hand sample is effectively normal.
Noah,
Solid write up, I posted some comments on that one. Please keep this series up (or something as wonk’ish). Its great seeing this much effort put into empirical poker work.
Can you tell about RAZZ stats?
because it is known as a “low variance game”
Hi Alvaro,
If you’d like to provide me data for razz, I’d be happy to do it. See this post.
Awesome post, Noah. TYVM
Hi Noah,
thanks for your work and sharing the crucial facts with, as you described ;), the less nerdy group of players.
Could you please make a simulation for a winrate of 0,5 BB which is pretty a standard one in 20BB CAP tables. It would help me a lot as I plan to go for an Elite at PS grinding it out at those CAP tables and I better know what to expect, also in terms of a proper bankroll.
Awesome post, thanks.
I think the best thing to take away from this article is that mass-tabling probably just lends itself to more vicious downswings rather than reducing it. The fact that a 2bb/100 winner is just as likely to lose over 250k hands as a 10bb/100 player is over 10k hands really hits home.
I strongly believe after reading this that 4-6 tabling effectively is the best way to avoid soul-crushing downswings rather than the more intuitive “play as many hands as possible to get to the long run asap” approach.
I remember reading once that someone said “One of the hardest thing I’ve ever done was be a mediocre poker player”. I think this article really illustrates that point perfectly.
please keep it up. You have perfect, easy to read and comprehend detail. BR, 180s, 45s, HU cash/SnG, full ring cash, more MTT…I’d love to see your thoughts on any of it. i have about 2m hands, mostly turbo 180s and MTTs. contact me if you need anything. and thank you again
“You can improve the statistics a little bit by using your AIEV bb/100 instead of your real bb/100. When I do that with my own data, it shrinks confidence intervals by about 25%.”
Can you explain how did you get that 25%?
Seconding Antani’s comment, I’d be interested.
Also, it would be very useful to many people if you added some addendum regarding rakeback, and the effect that has when paired with various winrates.
What I’m interested in:
How does the variance look for a 5bb/100 winner with 0% rakeback, versus a 0bb/100 winner with rakeback equivalent to 5bb/100? Does having a normally distributed 0bb winrate + monthly cash injection change anything? I would think so, but how much?I’d love to see the numbers worked out on that.
Daniel,
Rakeback doesn’t affect statistics because it’s already a component of the winrate.
I think ignoring rakeback when considering your winrate is an error
For example:
On your site you pay 5bb/100 as rake and you have a 40% deal.
You have a 4bb/100 winrate on your results.
The winrate you should use is 6bb/100 (4bb/100 plus the 2bb/100 of rakeback).
I hope I explained myself well